Derniers sujets
Qui est en ligne ?
Il y a en tout 0 utilisateur en ligne :: 0 Enregistré, 0 Invisible et 0 Invité :: 1 Moteur de rechercheAucun
Le record du nombre d'utilisateurs en ligne est de 29 le Mer 25 Fév 2015 - 14:01
Connexion
Statistiques
Nous avons 243 membres enregistrésL'utilisateur enregistré le plus récent est paul225l
Nos membres ont posté un total de 8922 messages dans 811 sujets
Une découverte probablement majeure pour la 3D sur Oric !!
Forum Oric :: Forums :: Forum Public :: Autres discussions
Page 1 sur 1
 Une découverte probablement majeure pour la 3D sur Oric !!
Une découverte probablement majeure pour la 3D sur Oric !!
Une découverte incroyable vient probablement d'être faite dans les laboratoires de recherche en charge du projet glOric.
En effet, une équipe de chercheur a récemment découvert que:
lorsque abs(X)>abs(Y) , SQRT(X^2 + Y^2) est à peu près égal à abs(X) + abs(Y) * (sqrt(2) -1)
Dingue !!
Cette découverte est de nature à considérablement faire chuter le nombre de cycle consommés par les routines du moteur de glOric.
En effet, glOric repose sur deux opérateurs pour ses projections de la 3D vers la 2D écran:
Hé bien c'est justement ce deuxième opérateur qui risque de se prendre une méchante accélération.
Les opérations d'élévation au carré et d'extraction de racine sont hyper chronophages ..
Et grâce à cette découverte, elles vont pouvoir être remplacées par une multiplication par une constante (qui pourra être mise en abaque ) et une addition
Je vous raconte pas la gueule du compteur de cycle ..
Interrogé en marge de l'annonce officielle de cette découverte, le responsable communication a expliqué:
Il a ensuite ajouté:
En effet, une équipe de chercheur a récemment découvert que:
lorsque abs(X)>abs(Y) , SQRT(X^2 + Y^2) est à peu près égal à abs(X) + abs(Y) * (sqrt(2) -1)
Dingue !!
Cette découverte est de nature à considérablement faire chuter le nombre de cycle consommés par les routines du moteur de glOric.
En effet, glOric repose sur deux opérateurs pour ses projections de la 3D vers la 2D écran:
- une arctangente (au sujet duquel l'auteur vous a déjà bien bourré le mou :-)
- un calcul de norme euclidienne basée sur une racine carré et deux élévations au carré.
Hé bien c'est justement ce deuxième opérateur qui risque de se prendre une méchante accélération.
Les opérations d'élévation au carré et d'extraction de racine sont hyper chronophages ..
Et grâce à cette découverte, elles vont pouvoir être remplacées par une multiplication par une constante (qui pourra être mise en abaque ) et une addition
Je vous raconte pas la gueule du compteur de cycle ..
Interrogé en marge de l'annonce officielle de cette découverte, le responsable communication a expliqué:
jbperin a écrit:
Après la sortie de la démo pour René, l'équipe de recherche et développement restait dubitative malgré le bon accueil d'une partie de la communauté. Les équipes en charge du rendu 2D se plaignaient du peu de moyen dont ellels disposaient. Aujourd'hui, cette découverte apporte un immense bol d'air. Le budget cycle dégagé grâce à cette découverte va pouvoir être réaffecter à la rasterization. C'est le projet entier qui va y gagner
Il a ensuite ajouté:
jbperin a écrit:
Bon .. c'est pas le tout mais va falloir coder le merdier maintenant .. vous savez s'il reste du champagne au buffet ?

jbperin- Messages : 132
Date d'inscription : 05/11/2019
Localisation : Drôme
 Re: Une découverte probablement majeure pour la 3D sur Oric !!
Re: Une découverte probablement majeure pour la 3D sur Oric !!
Bon ben les résultats viennent de tomber :
La bonne nouvelle: division par 3 du nombre de cycle !! une vraie tuerie. on passe de 1500 cycles pour projeter un point à 500 cycles.
Par contre, déconvenue : des aberrations de perspective apparaissent et l'effet fish eye est encore plus prononcé ..
==> voir si une partie des cycles économisés peut permettre de bricoler une compensation des distorsions.
L'aventure continue ...
La bonne nouvelle: division par 3 du nombre de cycle !! une vraie tuerie. on passe de 1500 cycles pour projeter un point à 500 cycles.
Par contre, déconvenue : des aberrations de perspective apparaissent et l'effet fish eye est encore plus prononcé ..
==> voir si une partie des cycles économisés peut permettre de bricoler une compensation des distorsions.
L'aventure continue ...

jbperin- Messages : 132
Date d'inscription : 05/11/2019
Localisation : Drôme
 Re: Une découverte probablement majeure pour la 3D sur Oric !!
Re: Une découverte probablement majeure pour la 3D sur Oric !!
Bonjour tout le monde,
Quelques nouvelles de mes avancées dans la recherche d'une routine de projection 3D super rapide.
J'en étais à m'attaquer à la norme euclidienne: z = sqrt (x^2 + y^2)
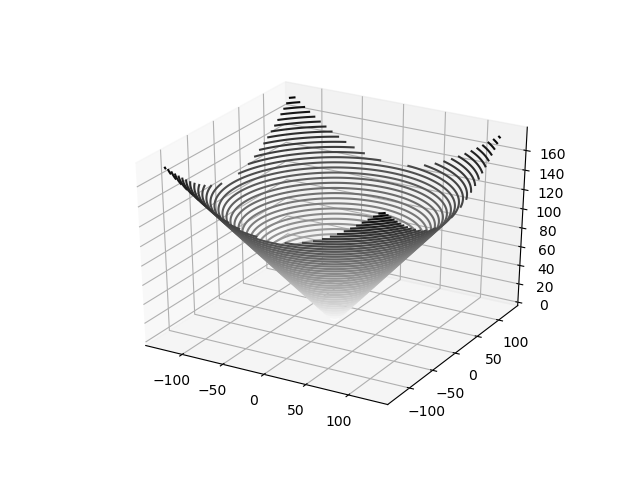
Cette fonction et symétrique, on peut se concentrer uniquement sur les valeurs positives de x et y.
Voici à quoi ressemble cette fonction sur l'espace des x et y positifs:
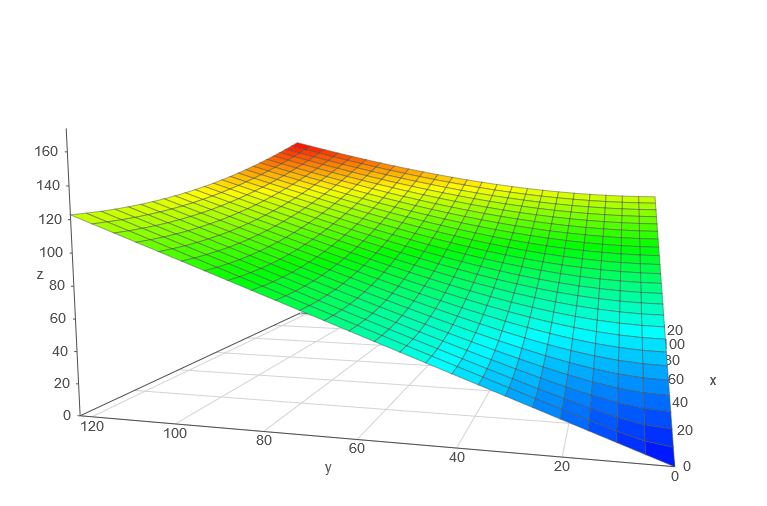
Comme c'est très "plat", ma première idée avait été de l'approximer par un plan en interpolant linéairement entre les axes x=0 et y=x par un algo de la forme:
Voici à quoi ressemble ce plan.
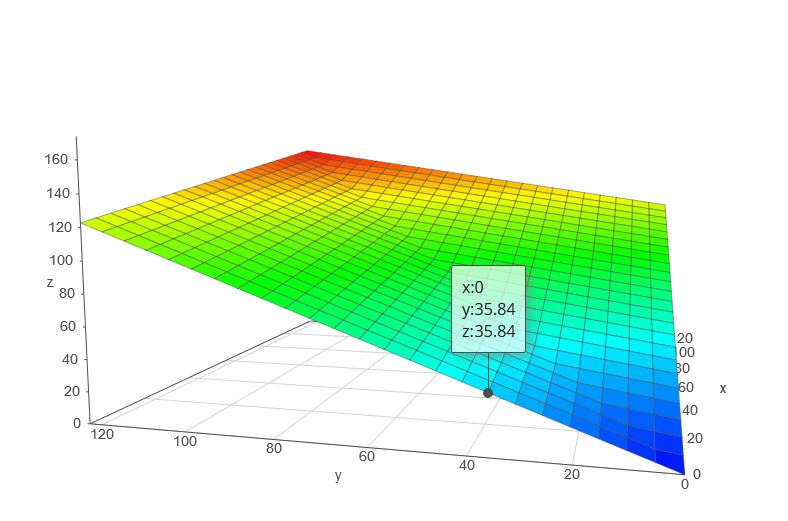
Obtenu en tapant :if (x>y, x + y * (sqrt(2) -1), y + x * (sqrt(2) -1)) sur academo.org
L'intérêt c'est que le calcul n'implique que:
- une comparaison
- un adressage indexé (pour la multiplication par une constante qu'on peut mettre en abbaque)
- une addition.
Mais il s'est avéré que l'approximation par un plan était trop imprécise comme le montre la figure suivante représentant la différence entre la valeur réelle et l'approximation par un plan.
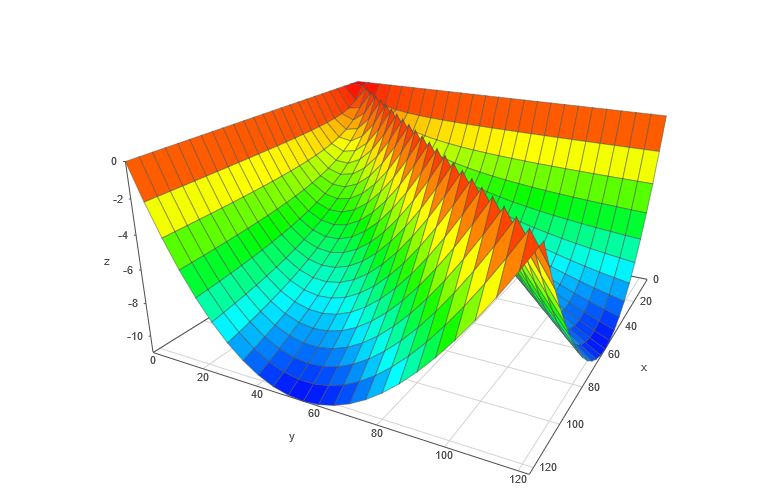
Obtenu en tapant :if (x>y, sqrt (x^2 + y^2) - (x + y * (sqrt(2) -1)), sqrt (x^2 + y^2) -(y + x * (sqrt(2) -1))) sur academo.org
L'erreur arrive à plus de 10 en valeur absolue.
Après avoir constaté que l'erreur était la plus grande au centre ma zone d'approximation (là où Y = X/2), j'ai décidé de faire une approximation par deux plans pluôt qu'un.
L'intérêt de cette forme reste qu'en assembleur, elle peut se réaliser par :
- deux comparaisons
- deux adressages indirect
- une somme
Par le calcul manuel je suis arrivé à :
Les résultats étaient déjà sympas comme le montre cette représentation de l'erreur (erreur inférieure à 3.5):
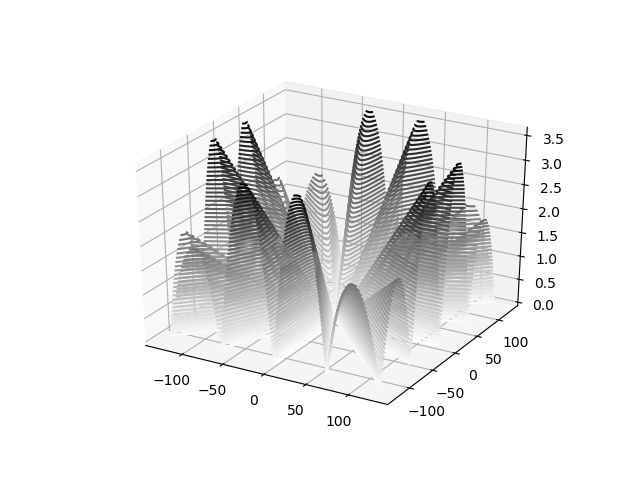
Mais je ne me suis pas arrêté là ..
J'ai utilisé cette combinaison de valeur comme point de départ d'une recherche de combinaison optimale, par regression linéaire des moindre carré sur l'erreur.
Et, puisque les tables de multiplication A, B, C et D allaient être des abbaques, je me suis dit qu'il était possible d'y mettre autre chose qu'une fonction affine. Et j'ai décidé de faire rechercher (par l'ordinateur du 21ème siècle) une fonction polynomiale du second ordre pour chaque table A B C et D
L'idée c'est de, tout en gardant le temps de calcul évoqué plus haut (puis que la fonction polynomiale sera mise en abbaque), disposer d'une fonction de calcul de la forme suivante:
Car un choix précis des coefficients A0, A1, A2, B0, B1, B2, C0, C1, C2, D0, D1, D2 permet aux erreurs de se compenser !!
L'erreur finale a cet aspect:
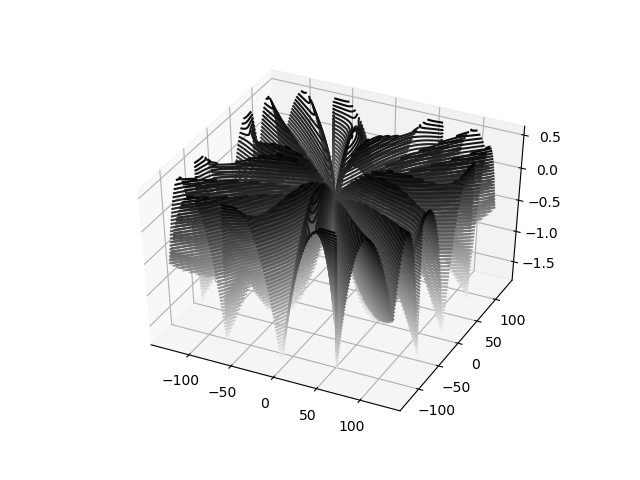
L'erreur est inférieure à 2 en valeur absolu et elle est un peu plus centrée autour de 0.
Après un tunning manuel de quelques valeurs proche de 0, je suis arrivé à une erreur inférieure à 11% (erreur d'arrondi comprise) sur tout le domaine de définition.
Il est possible d'aller encore plus loin dans la fidélité de l'approximation en utilisant un algo de backtracking pour le choix des arrondis.
Le choix d'une approximation biplanaire a permis de diviser par trois le temps de calcul de la norme euclidienne.
Sans trop sacrifier à la précision.
Retrouvez les outils utilisés, le abaques obtenues et le code utilisé sur le dépôt glOric sur Oric Software.
Pour avoir un rendu, télécharger les démos depuis le post de démo sur DefenseForce
Joyeux Noël à tous
Quelques nouvelles de mes avancées dans la recherche d'une routine de projection 3D super rapide.
J'en étais à m'attaquer à la norme euclidienne: z = sqrt (x^2 + y^2)

Cette fonction et symétrique, on peut se concentrer uniquement sur les valeurs positives de x et y.
Voici à quoi ressemble cette fonction sur l'espace des x et y positifs:
Comme c'est très "plat", ma première idée avait été de l'approximer par un plan en interpolant linéairement entre les axes x=0 et y=x par un algo de la forme:
- Code:
SI abs(x)>abs(y)
Z = abs(x) + abs(y) * (sqrt(2) -1)
SINON
Z = abs(x) + abs(y) * (sqrt(2) -1)
FINSI
Voici à quoi ressemble ce plan.
Obtenu en tapant :if (x>y, x + y * (sqrt(2) -1), y + x * (sqrt(2) -1)) sur academo.org
L'intérêt c'est que le calcul n'implique que:
- une comparaison
- un adressage indexé (pour la multiplication par une constante qu'on peut mettre en abbaque)
- une addition.
Mais il s'est avéré que l'approximation par un plan était trop imprécise comme le montre la figure suivante représentant la différence entre la valeur réelle et l'approximation par un plan.
Obtenu en tapant :if (x>y, sqrt (x^2 + y^2) - (x + y * (sqrt(2) -1)), sqrt (x^2 + y^2) -(y + x * (sqrt(2) -1))) sur academo.org
L'erreur arrive à plus de 10 en valeur absolue.
Après avoir constaté que l'erreur était la plus grande au centre ma zone d'approximation (là où Y = X/2), j'ai décidé de faire une approximation par deux plans pluôt qu'un.
- Code:
if ax >= ay:
x, y = ax, ay
else:
x, y = ay, ax
if y > x/2 :
Z = C*x + D*Y
else:
Z = A*x + B*y
L'intérêt de cette forme reste qu'en assembleur, elle peut se réaliser par :
- deux comparaisons
- deux adressages indirect
- une somme
Par le calcul manuel je suis arrivé à :
- Code:
A = 1.0
B = math.sqrt(5) - 2
C = math.sqrt(5)-math.sqrt(2)
D = 2*math.sqrt(2) - math.sqrt(5)
Les résultats étaient déjà sympas comme le montre cette représentation de l'erreur (erreur inférieure à 3.5):

Mais je ne me suis pas arrêté là ..
J'ai utilisé cette combinaison de valeur comme point de départ d'une recherche de combinaison optimale, par regression linéaire des moindre carré sur l'erreur.
Et, puisque les tables de multiplication A, B, C et D allaient être des abbaques, je me suis dit qu'il était possible d'y mettre autre chose qu'une fonction affine. Et j'ai décidé de faire rechercher (par l'ordinateur du 21ème siècle) une fonction polynomiale du second ordre pour chaque table A B C et D
L'idée c'est de, tout en gardant le temps de calcul évoqué plus haut (puis que la fonction polynomiale sera mise en abbaque), disposer d'une fonction de calcul de la forme suivante:
- Code:
if ax >= ay:
x, y = ax, ay
else:
x, y = ay, ax
if y > x/2 :
Z = C2 * (x^2) + C1 * x + C0 + D2 * (y^2) + D1 * y + D0
else:
Z = A2 * (x^2) + A1 * x + A0 + B2 * (y^2) + B1 * y + B0
Car un choix précis des coefficients A0, A1, A2, B0, B1, B2, C0, C1, C2, D0, D1, D2 permet aux erreurs de se compenser !!
L'erreur finale a cet aspect:

L'erreur est inférieure à 2 en valeur absolu et elle est un peu plus centrée autour de 0.
Après un tunning manuel de quelques valeurs proche de 0, je suis arrivé à une erreur inférieure à 11% (erreur d'arrondi comprise) sur tout le domaine de définition.
Il est possible d'aller encore plus loin dans la fidélité de l'approximation en utilisant un algo de backtracking pour le choix des arrondis.
Le choix d'une approximation biplanaire a permis de diviser par trois le temps de calcul de la norme euclidienne.
Sans trop sacrifier à la précision.

Retrouvez les outils utilisés, le abaques obtenues et le code utilisé sur le dépôt glOric sur Oric Software.
Pour avoir un rendu, télécharger les démos depuis le post de démo sur DefenseForce
Joyeux Noël à tous

jbperin- Messages : 132
Date d'inscription : 05/11/2019
Localisation : Drôme
Euchcat aime ce message
Forum Oric :: Forums :: Forum Public :: Autres discussions
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum|
|
|










» Bla Bla général du Jury
» carte mère Oric (re)tracée
» Meurtre à Grande Vitesse
» ORIC-1 sur LE BON COIN
» ORIC ATMOS sur LE BON COIN
» Problème d'affichage des couleurs avec un Oric Atmos
» Bienvenue dans le Forum des Oriciens
» Rencontre avec Laurant Weill, co-fondateur de Loriciel, et mon garçon de 12 ans
» Bonnes fêtes
» Murders in Venice / Meutres à Venise
» Un clavier PS/2 pour tester un ORIC
» Disquette 3" Sedoric
» faire un 6502 avec des phototransistor
» Oricutron linux et DSK